【連続投稿88日目 1727投稿目】
【作成日時:10/14 25:11~25:36、25分】
【らくだプリント 中2-38(続き)】
itasan-kibunyasan.hatenablog.com
一昨日の投稿で「わかる」と「できる」の連動という話をしました。
そこでは、表を埋めること、座標を取ることのそれぞれの部分において繰り返し取り組むことで「できる」→「わかる」となることを書きました。
しかしこの話の時には、式から表を埋めること、表から座標を取ること、座標を取ることからグラフを描くこと、といった2要素の関係性については触れていませんでした。
今日はそのような関数の単元を構成する要素の関係性に注目してみましょう。
昨日と同じ38番のプリントの話になりますが、このプリントの後半の問題はシンプルです。
描かれているグラフから切片と傾きを読み取ることでグラフの式を求める問題になっています。
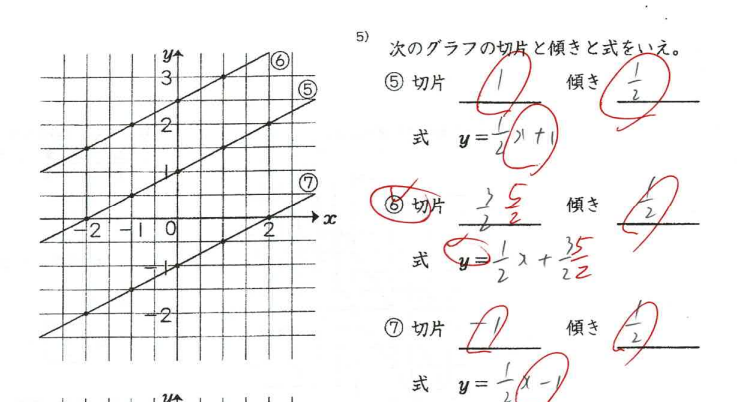
このような問題だけであれば単純なのですが、一昨日の投稿にも書いた
これは学校や学習塾で働いていて驚いたことなのですが、方程式は簡単に解けるけれども関数は同じ程度の基礎の問題でも分からないという子が何人もいたのでした。
というようなことが現れるのは、テストになった時なのですよね。
プリントのように学習することとテストの違いはというと、いろんな形式の問題が混ざっているかどうかにあります。
混ざっているとできなくなるのはなぜでしょう?
それが構成する要素の間にある関係性を「わかる」ことにあるのです。
関係性がわかる人にとってはグラフは式を視覚化したものであり、式はグラフを数式化したものということがわかっています。
ですがそれがわかっていないと、さらに関数を構成する要素が増えた時にこの関係性が絡まって、ほどき明かせないのです。
ですから要素間の関係性については「わかる」→「できる」の流れでつかむことも必要となるのです。
これが関数より前の単元にはほとんどなかったことになります。
ですから関数においてはわかったつもりになっていることは危険です。
立ち止まらないと八方ふさがりに遭ってしまいます。
----------------------------
今後のイベント予定
11/17(日)13:00~17:00 経営ゲーム塾B @寺子屋塾
12月(日程調整中)10:00~17:00 ワンデイ経営ゲーム塾 @寺子屋塾 ※経験者限定
☆定点観測を一緒に取り組みたい人、随時募集中です(^ ^) 定点観測についてはこちらをどうぞ!
☆個別インタビューゲームについても随時募集中です!